Unit 1: Kinematics Summary
Part 1: 1.0-1.4
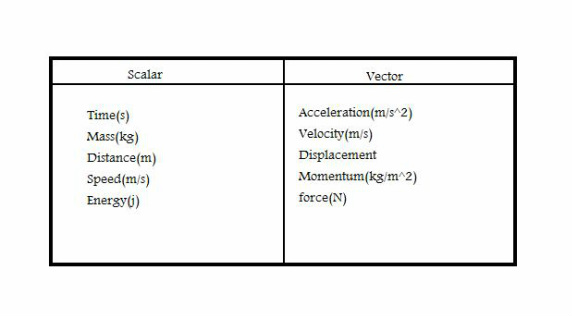
The first unit we looked at in our journey through physics 20 is Kinematics. This unit is the study motion, in other words this unit is a field of science that describes how an object or system creates forces that causes motion. Kinematics is special in particular because it was the stepping stone for us in physics 20 and what we learned in Kinematics we also applied in other chapters. Strangely enough one particular force that wasn't heavily focused on in this chapter was the force of gravity.We only saw it during projectile motion because it brought in the concept of vertical, compared to objects that were on flat horizontal surfaces. Two very important concepts were introduced in this unit being scalar and vector quantities. Scalar being quantities without direction, compared to vector quantities which have direction indicated by the little arrow overheard of the symbol.
Scalar:
· t = Time
· d = Distance
s=Speed
Vector:
· v = Velocity
· vf = Final Velocity
· vi = Initial Velocity
· a = Acceleration
· d = Displacement
There is a lot of terminology that you must memorize.
Distance: The total amount a person has traveled, this corresponds with time. Both distance and displacement are measured in centimeters (cm) meters (m) and kilometers (km).
Displacement: Is how far an object has traveled, its the objects change in position from the origin.
Uniform Motion: Constant velocity or speed at rest or in motion
Non-uniform Motion: When the direction or speed of an object changes or is inconsistent
Uniformly Accelerated Motion: Acceleration is uniform throughout the motion, ex an object moving at a constant 5 m/s^2
Tangent: The tangent of the distance time graph (D/T) is instantaneous velocity.
Instantaneous Velocity: Is the velocity at a specific point in time, its found by doing rise over run (Y divided by X).
Projectile Motion: Is a form of motion that is created by throwing an object near the earth’s surface and creates a curved path because of gravity.
Acceleration: Is the rate that an object is increasing its speed at, measured in m/s^2
Scalar Quantity: Are quantities that have no direction. Time, distance and speed.
Vector Quantity: Are quantities that have direction. Velocity, displacement and acceleration.
Velocity: The speed and direction of an object in motion. Measured in m/s.
Speed: The speed is how fast an object is moving which is measured in m/s. Do not confuse with velocity, because velocity has direction and speed does NOT.
Graphs
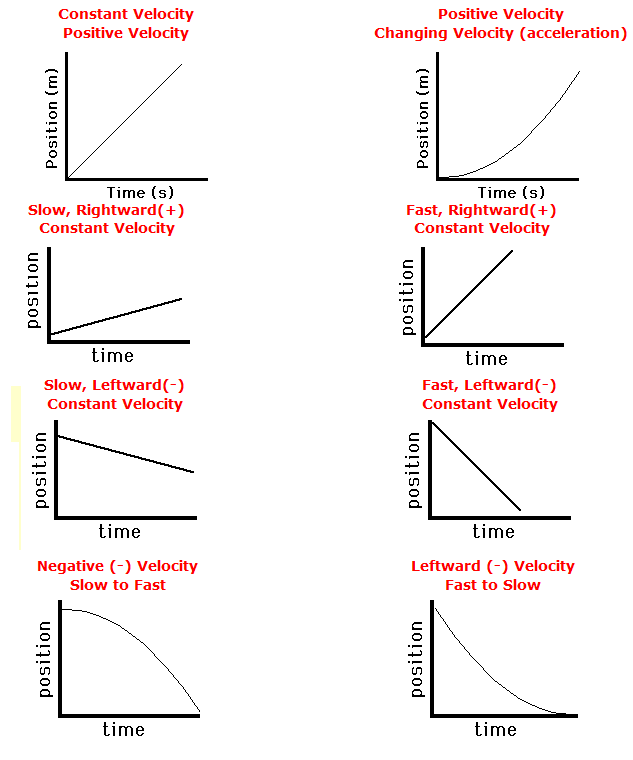
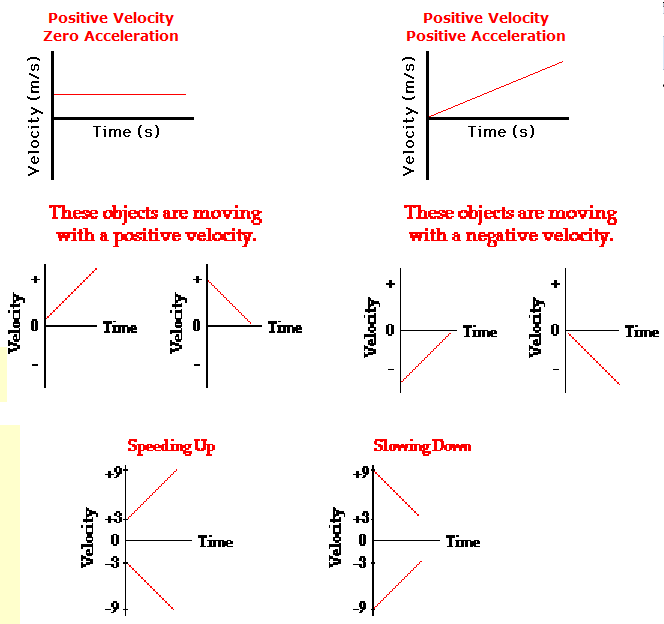
We focused on primarily two different types of graphs in physics 20. Position/Time graphs (measured in meters) and Velocity/Time graphs ( measured in m/s ). Both graphs represent two different ideas, for instance the slope of a velocity time graph represents acceleration and the area under the graph totaled up will represent displacement. While in a position time graph the slope will represent the velocity of the graph. At the same time you can find instantaneous velocity of a position time graph by doing the ( Y / X ) rise over run. Here are examples of the graphs.
The first unit we looked at in our journey through physics 20 is Kinematics. This unit is the study motion, in other words this unit is a field of science that describes how an object or system creates forces that causes motion. Kinematics is special in particular because it was the stepping stone for us in physics 20 and what we learned in Kinematics we also applied in other chapters. Strangely enough one particular force that wasn't heavily focused on in this chapter was the force of gravity.We only saw it during projectile motion because it brought in the concept of vertical, compared to objects that were on flat horizontal surfaces. Two very important concepts were introduced in this unit being scalar and vector quantities. Scalar being quantities without direction, compared to vector quantities which have direction indicated by the little arrow overheard of the symbol.
Scalar:
· t = Time
· d = Distance
s=Speed
Vector:
· v = Velocity
· vf = Final Velocity
· vi = Initial Velocity
· a = Acceleration
· d = Displacement
There is a lot of terminology that you must memorize.
Distance: The total amount a person has traveled, this corresponds with time. Both distance and displacement are measured in centimeters (cm) meters (m) and kilometers (km).
Displacement: Is how far an object has traveled, its the objects change in position from the origin.
Uniform Motion: Constant velocity or speed at rest or in motion
Non-uniform Motion: When the direction or speed of an object changes or is inconsistent
Uniformly Accelerated Motion: Acceleration is uniform throughout the motion, ex an object moving at a constant 5 m/s^2
Tangent: The tangent of the distance time graph (D/T) is instantaneous velocity.
Instantaneous Velocity: Is the velocity at a specific point in time, its found by doing rise over run (Y divided by X).
Projectile Motion: Is a form of motion that is created by throwing an object near the earth’s surface and creates a curved path because of gravity.
Acceleration: Is the rate that an object is increasing its speed at, measured in m/s^2
Scalar Quantity: Are quantities that have no direction. Time, distance and speed.
Vector Quantity: Are quantities that have direction. Velocity, displacement and acceleration.
Velocity: The speed and direction of an object in motion. Measured in m/s.
Speed: The speed is how fast an object is moving which is measured in m/s. Do not confuse with velocity, because velocity has direction and speed does NOT.
Graphs
We focused on primarily two different types of graphs in physics 20. Position/Time graphs (measured in meters) and Velocity/Time graphs ( measured in m/s ). Both graphs represent two different ideas, for instance the slope of a velocity time graph represents acceleration and the area under the graph totaled up will represent displacement. While in a position time graph the slope will represent the velocity of the graph. At the same time you can find instantaneous velocity of a position time graph by doing the ( Y / X ) rise over run. Here are examples of the graphs.
Part 2 2.0-2.3
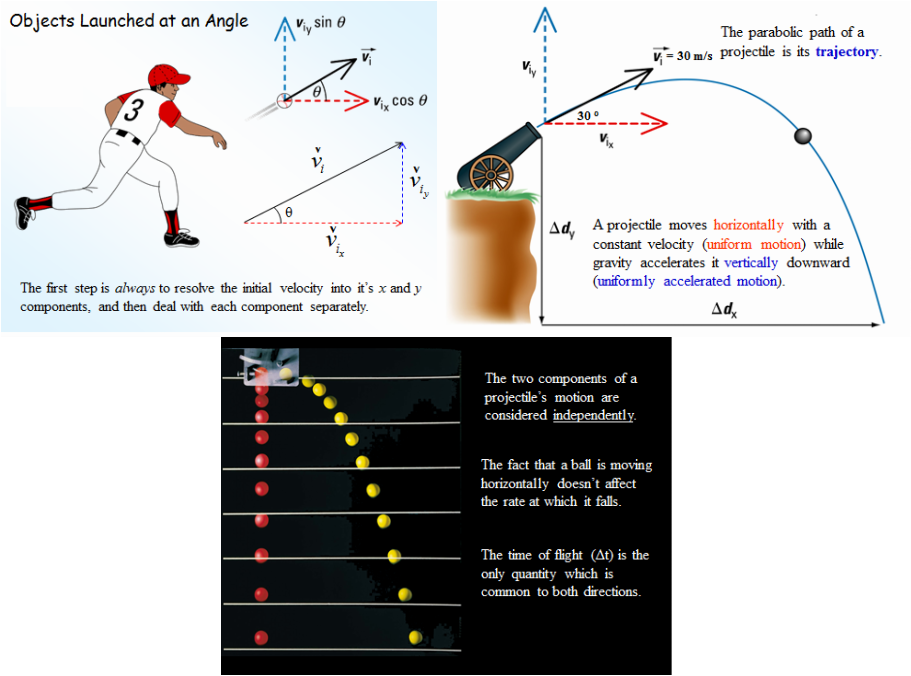
The second part of the unit deals with projectile motion and reading visual graphs for displacement of objects. This is demonstrated by East/South (-) and West/North (+) directions. An example of this is would be a person travelling 5 meters East then traveling 5 meters West. This person has traveled a total displace of 0 meters, but a total distance of 10 meters. Now the major part of the unit, projectile motion, this was first founded by Galileo and he found that objects move in two directions, X horizontal direction and Y vertical direction.
Key Notes
· Acceleration due to Gravity is equal to 9.81 m/s^2
· Final velocity of an object is its highest point it reaches in the Y direction
· Projectile path is a parabola
· To solve problems involving projectiles, first resolve the motion of its components (X and Y) using the trigonometric functions, then apply the kinematic equations
· At a vertical direction a projectiles velocity is the greatest the instant it leaves rest and just before impact. At the highest point velocity will be zero.
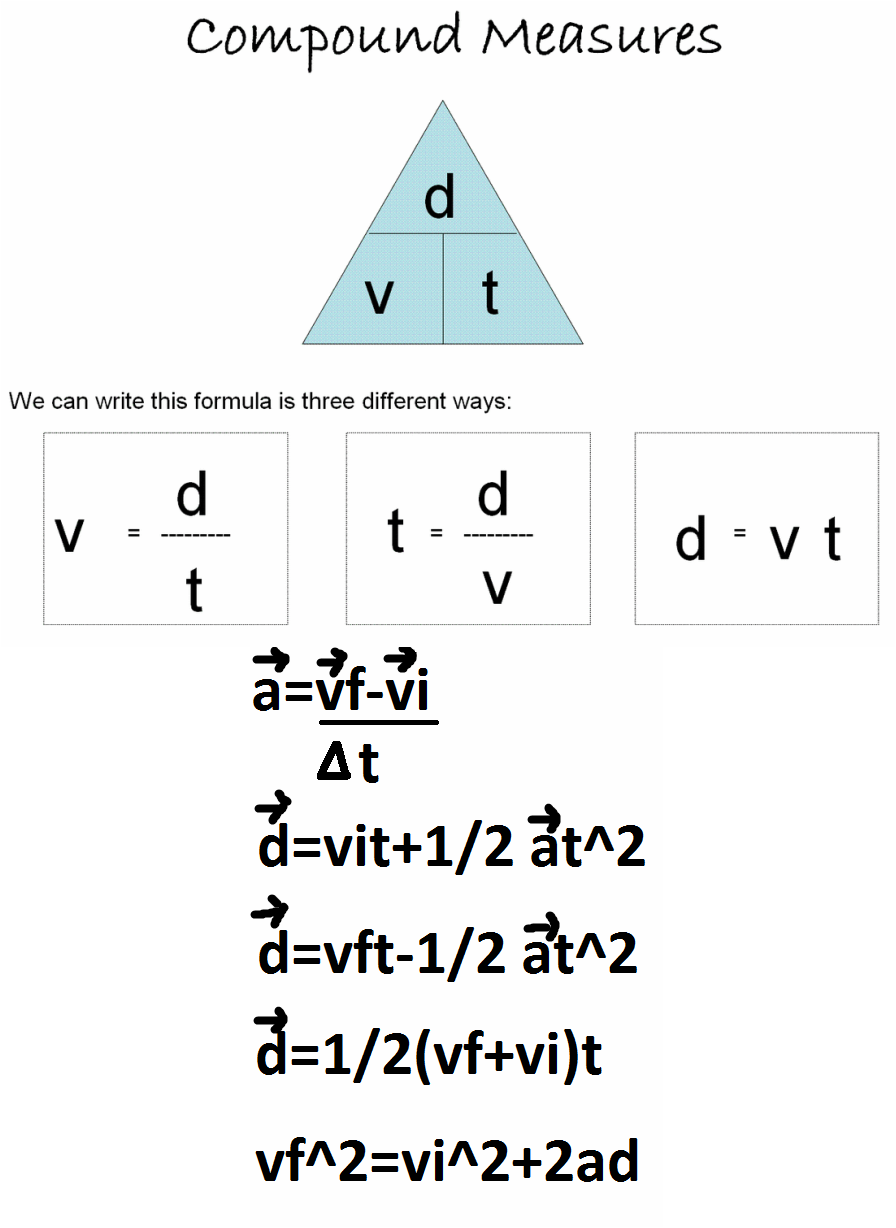
Below are the 6 formulas in Kinematics
Key Notes
· Acceleration due to Gravity is equal to 9.81 m/s^2
· Final velocity of an object is its highest point it reaches in the Y direction
· Projectile path is a parabola
· To solve problems involving projectiles, first resolve the motion of its components (X and Y) using the trigonometric functions, then apply the kinematic equations
· At a vertical direction a projectiles velocity is the greatest the instant it leaves rest and just before impact. At the highest point velocity will be zero.
Below are the 6 formulas in Kinematics
Unit 1: Kinematics Example Problems
Key notes:
Units
Significant digits
Formulas
Converting km/h to m/s
In the X direction you will only use v = d/t in projectile motion
1. Compare and contrast distance and displacement.
Answer: Distance is a scalar vector, meaning it has no direction. Displacement is a vector quantity meaning it has direction. Both are measured in meters and are dependent on time.
2. To perform a give and go, a basketball player fakes out the defense by moving .75m right and then 3.5m left. What is the player’s displacement from the starting position?
Answer: 3.5m left - .75m right = 2.75m left.
3. While building a wall, a bricklayer sweeps the cement back and forth. If she swings her hand back and forth, a distance of 1.70m, four times, calculate the distance and displacement her hand travels during that time.
Answer: 1.70m x 4 = 6.80 meters distance, 0m displacement. The reason she has a zero displacement because her hand did not move from the original position after she was finished.
4. Can objects have the same speed but different velocities?
Answer: Yes, one of the objects can be going east while the other is heading west.
5. A camper kayaks 16 km E from a camping site, stops, and then paddles 23k W. What is the camper’s final position with respect to the campsite?
Answer: 23km west – 16 km east = 8km west. His position is 8 km west from the campsite.
6. Two children on racing bikes start from the same reference point. Child A travels 5.0 m/s right and child B travels 4.5 m/s right. How much further did child A travel than B after 5.0s?
Answer:
5 m/s x 5s = 25m right.
5 m/s x 4.5 = 22.5m right
25m – 22.5m = 2.5m right
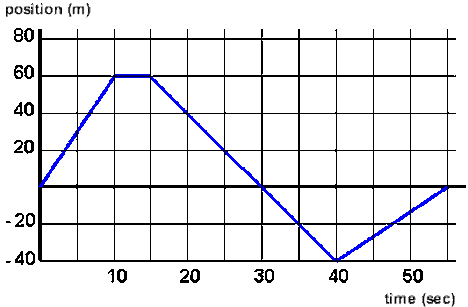
7. Describe the motion that is being shown in the graph below.
Answer: The pole is the origin. A man starts to sprint from a pole towards a fence, stops and turns around but sprints back with half the speed and runs past the pole towards a sandbox, turns around and jog back towards the pole.
Answer: Distance is a scalar vector, meaning it has no direction. Displacement is a vector quantity meaning it has direction. Both are measured in meters and are dependent on time.
2. To perform a give and go, a basketball player fakes out the defense by moving .75m right and then 3.5m left. What is the player’s displacement from the starting position?
Answer: 3.5m left - .75m right = 2.75m left.
3. While building a wall, a bricklayer sweeps the cement back and forth. If she swings her hand back and forth, a distance of 1.70m, four times, calculate the distance and displacement her hand travels during that time.
Answer: 1.70m x 4 = 6.80 meters distance, 0m displacement. The reason she has a zero displacement because her hand did not move from the original position after she was finished.
4. Can objects have the same speed but different velocities?
Answer: Yes, one of the objects can be going east while the other is heading west.
5. A camper kayaks 16 km E from a camping site, stops, and then paddles 23k W. What is the camper’s final position with respect to the campsite?
Answer: 23km west – 16 km east = 8km west. His position is 8 km west from the campsite.
6. Two children on racing bikes start from the same reference point. Child A travels 5.0 m/s right and child B travels 4.5 m/s right. How much further did child A travel than B after 5.0s?
Answer:
5 m/s x 5s = 25m right.
5 m/s x 4.5 = 22.5m right
25m – 22.5m = 2.5m right
7. Describe the motion that is being shown in the graph below.
Answer: The pole is the origin. A man starts to sprint from a pole towards a fence, stops and turns around but sprints back with half the speed and runs past the pole towards a sandbox, turns around and jog back towards the pole.
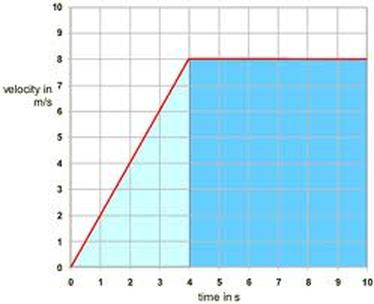
8. Explain what is occurring in the graph below.
Answer: A man accelerates to 8 m/s east and stays at the constant velocity.
Answer: A man accelerates to 8 m/s east and stays at the constant velocity.
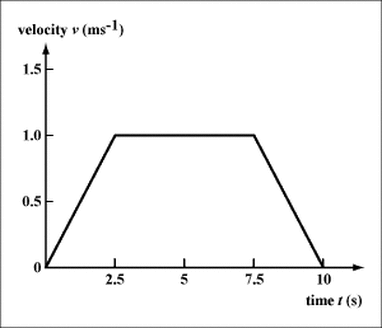
9. Calculate the displacement from the velocity time graph below
Answer:
1 x 2.5 / 2 = 1.25m east
5 x 1 = 5.00m east
1 x 2.5 / 2 = 1.25m east
1.25m + 1.25m + 5.00m = 7.5m east
10. A motorcycle with an initial velocity 6.0 m/s east accelerates at 4.0 m/s ^ 2 east. How long will it take the motorcycle to reach a final velocity of 36.0 m/s east?
Answer:
t = vf – vi / a
t = 36 m/s – 6.0 m/s / 4.0 m/s ^ 2
t = 7.5 s
11. An elk moving at a velocity of 20km/h north accelerates at 1.5 m/s ^ 2 north for 9.3 seconds until it reaches its maximum velocity. Calculate its maximum velocity, in km/h.
Answer: Convert to m/s then back to km/h
a = vf - vi / t
vf = at + vi
vf = 1.5 m/s ^ 2 x 9.3s + 5.56 m/s east
19.5 m/s east x 3.6 = 70 km/h
12. A hound running at a velocity of 16 m/s south slows down uniformly to a velocity of 4.0 m/s south in 4.0 s. What is the displacement of the hound during this time?
Answer:
d = ½ (vf+vi)t
d = ½ (16 m/s south + 4 m/s south) 4.0 s
d= 40 m south
13. A skier is moving down a uniform slope at 3.0 m/s. If the acceleration down the hill is 4.0 m/s ^ 2, find the skier’s displacement after 5.0 seconds.
Answer:
d = vit + ½ at^2
d= 3.0 m/s x 5s + ½ 4.0 m/s^2 x 5s^2
d =65 m down
14. If a car needs to increase its speed from 50 km /h to 100 km /h and the engine can provide a maximum acceleration of magnitude 3.8 m/s, find the minimum length of the on-ramp
Answer: Convert km/h to m/s
d = vf^2 – vi^2 / 2a
d = 27.78^2 – 13.88^2 / 2 x 3.8 m/s^2
d = 76m
15. What is the displacement of a logging truck accelerating from 10 m/s right to 20 m/s right in 5.0s
Answer:
d = ½( vf + vi )t
d = ½( 20 m/s right + 10 m/s right ) x 5.0 s
d = 75m
16. An elevator moving downward at 4.0 m’s experiences an upward acceleration of 2.00 m/s ^ 2 for 1.80 s. What is its velocity at the end of the acceleration and how far has it traveled.
Answer: Note moving downward velocity and moving upward acceleration.
Part 1
vf = a x t – vi
vf = 2.00 m/s ^ 2 x 1.80 s – 4 m/s
vf = .400 m/s
Part 2
d = ½( vf + vi ) t
d = ½ ( .400 m/s south + 4.00 m/s south ) x 1.80 s
d = 3.96m
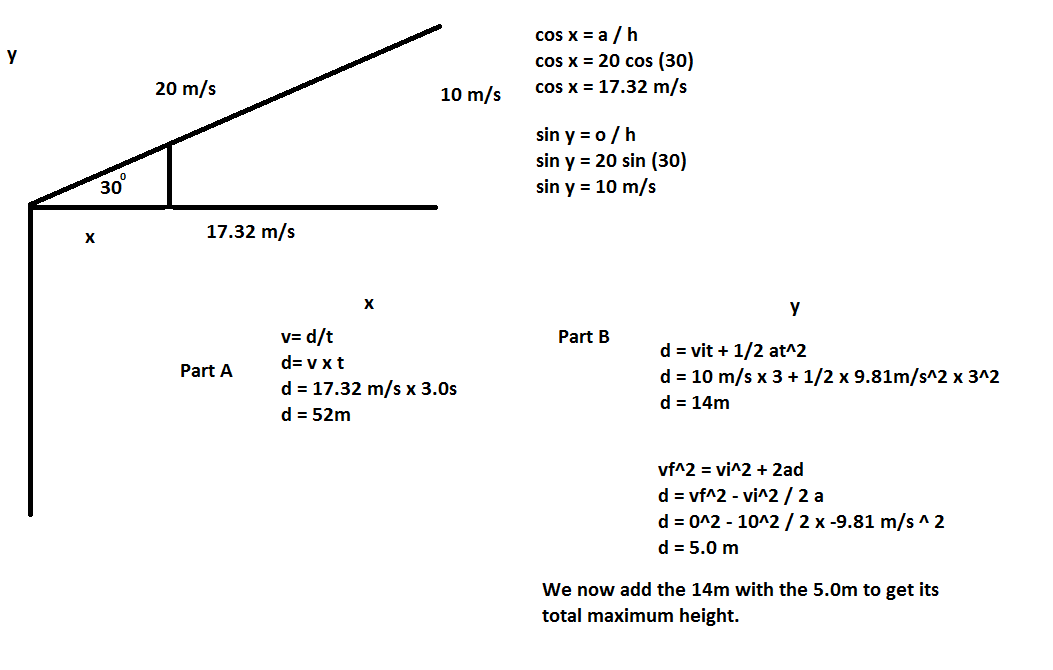
17. A ball is thrown with a velocity of 20.0 m/s [30 degrees] and travels for 3.0s before it strikes the ground. Find the distance it ravels horizontally, the height from which it was thrown and the maximum height of the ball.
Answer
Answer:
1 x 2.5 / 2 = 1.25m east
5 x 1 = 5.00m east
1 x 2.5 / 2 = 1.25m east
1.25m + 1.25m + 5.00m = 7.5m east
10. A motorcycle with an initial velocity 6.0 m/s east accelerates at 4.0 m/s ^ 2 east. How long will it take the motorcycle to reach a final velocity of 36.0 m/s east?
Answer:
t = vf – vi / a
t = 36 m/s – 6.0 m/s / 4.0 m/s ^ 2
t = 7.5 s
11. An elk moving at a velocity of 20km/h north accelerates at 1.5 m/s ^ 2 north for 9.3 seconds until it reaches its maximum velocity. Calculate its maximum velocity, in km/h.
Answer: Convert to m/s then back to km/h
a = vf - vi / t
vf = at + vi
vf = 1.5 m/s ^ 2 x 9.3s + 5.56 m/s east
19.5 m/s east x 3.6 = 70 km/h
12. A hound running at a velocity of 16 m/s south slows down uniformly to a velocity of 4.0 m/s south in 4.0 s. What is the displacement of the hound during this time?
Answer:
d = ½ (vf+vi)t
d = ½ (16 m/s south + 4 m/s south) 4.0 s
d= 40 m south
13. A skier is moving down a uniform slope at 3.0 m/s. If the acceleration down the hill is 4.0 m/s ^ 2, find the skier’s displacement after 5.0 seconds.
Answer:
d = vit + ½ at^2
d= 3.0 m/s x 5s + ½ 4.0 m/s^2 x 5s^2
d =65 m down
14. If a car needs to increase its speed from 50 km /h to 100 km /h and the engine can provide a maximum acceleration of magnitude 3.8 m/s, find the minimum length of the on-ramp
Answer: Convert km/h to m/s
d = vf^2 – vi^2 / 2a
d = 27.78^2 – 13.88^2 / 2 x 3.8 m/s^2
d = 76m
15. What is the displacement of a logging truck accelerating from 10 m/s right to 20 m/s right in 5.0s
Answer:
d = ½( vf + vi )t
d = ½( 20 m/s right + 10 m/s right ) x 5.0 s
d = 75m
16. An elevator moving downward at 4.0 m’s experiences an upward acceleration of 2.00 m/s ^ 2 for 1.80 s. What is its velocity at the end of the acceleration and how far has it traveled.
Answer: Note moving downward velocity and moving upward acceleration.
Part 1
vf = a x t – vi
vf = 2.00 m/s ^ 2 x 1.80 s – 4 m/s
vf = .400 m/s
Part 2
d = ½( vf + vi ) t
d = ½ ( .400 m/s south + 4.00 m/s south ) x 1.80 s
d = 3.96m
17. A ball is thrown with a velocity of 20.0 m/s [30 degrees] and travels for 3.0s before it strikes the ground. Find the distance it ravels horizontally, the height from which it was thrown and the maximum height of the ball.
Answer