Unit 2: Dynamics
In Unit 2, we learned about how dynamics deals with the effects of forces on objects. This is vital because structures that move, IE bridges and buildings must move in appropriate ways, depending on the design, so that they are safe to use. In this section we dealt with many types of forces such as force of gravity, normal force, force of friction and total force of an object. We also dealt with 3 of newtons laws, how friction affects motion and gravitational forces due to mass objects in space.
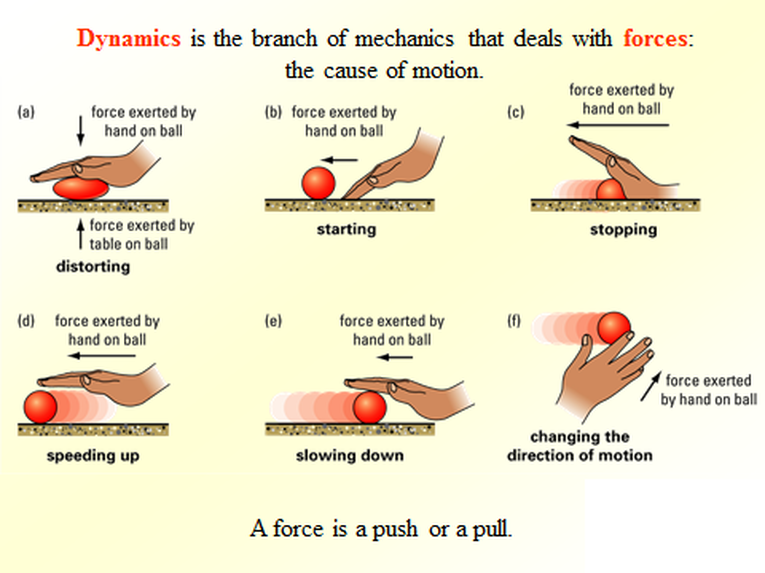
What is force? A force is a push or pull. If one object exerts a force on another, the second object exerts an equal and opposite force on the first. The Earth accelerates the fruit more than the fruit accelerates the Earth because the Earth has more mass and is harder to move.
Remember! Weight and mass are not the same! The acceleration of an elevator can simulate higher and lower gravity, as it pushes you up and down. When the force of gravity changes, your weight changes, but your mass is always the same.
Terminology
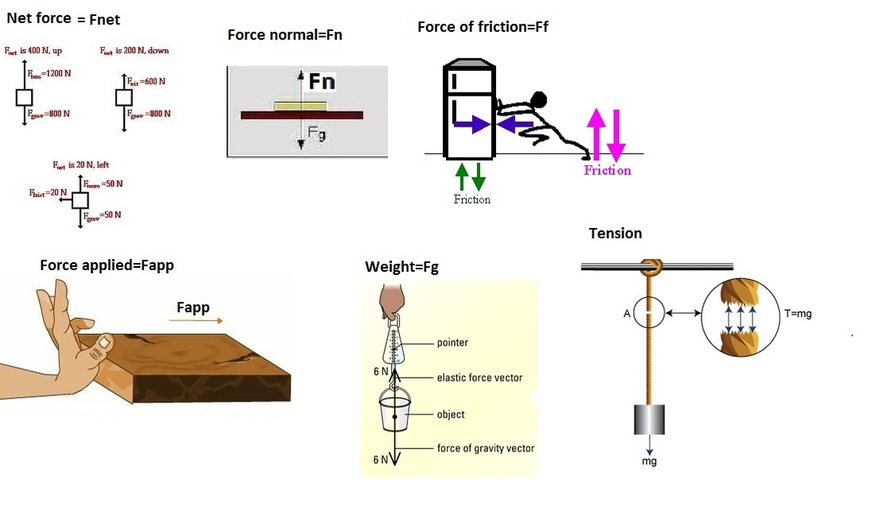
Weight - The force that gravity exerts on an object
Free-body diagram - is a vector diagram that shows all the forces exerted on an object
Dynamics - branch of mechanics that deals with forces
Normal force - is the force that a surface exerts on an object that is resting on it
Applied force - Any push or pull of an object
Net force - the vector sum of all forces acting on an object
Force of friction - Friction always opposes the motion or attempted motion of one surface across another surface. Friction is dependent on the texture of both surfaces. Friction is also dependent on normal force.
Tension - force applied through pulling a rope
Inertia - is the resistance of any physical object to a change in its state of motion or rest
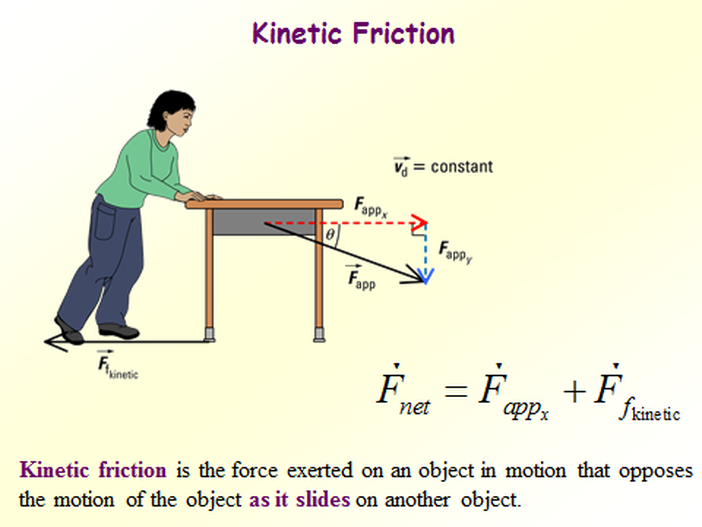
Kinetic friction - Kinetic friction is the force between two objects that are moving relative to each other.
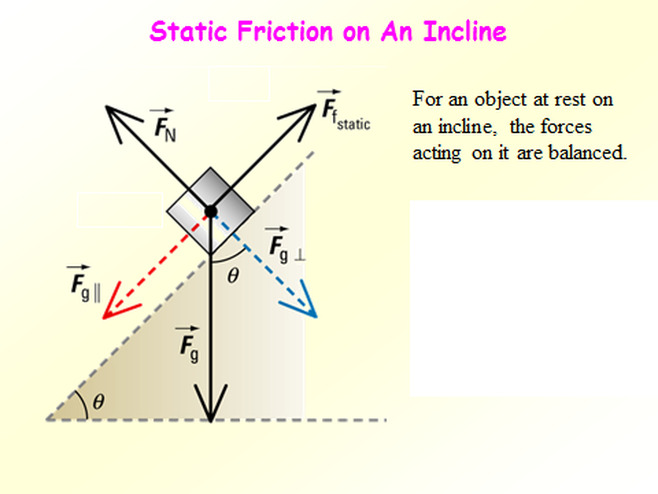
Static friction - Is the force of friction that keeps an object stationary so it does not move.
What is force? A force is a push or pull. If one object exerts a force on another, the second object exerts an equal and opposite force on the first. The Earth accelerates the fruit more than the fruit accelerates the Earth because the Earth has more mass and is harder to move.
Remember! Weight and mass are not the same! The acceleration of an elevator can simulate higher and lower gravity, as it pushes you up and down. When the force of gravity changes, your weight changes, but your mass is always the same.
Terminology
Weight - The force that gravity exerts on an object
Free-body diagram - is a vector diagram that shows all the forces exerted on an object
Dynamics - branch of mechanics that deals with forces
Normal force - is the force that a surface exerts on an object that is resting on it
Applied force - Any push or pull of an object
Net force - the vector sum of all forces acting on an object
Force of friction - Friction always opposes the motion or attempted motion of one surface across another surface. Friction is dependent on the texture of both surfaces. Friction is also dependent on normal force.
Tension - force applied through pulling a rope
Inertia - is the resistance of any physical object to a change in its state of motion or rest
Kinetic friction - Kinetic friction is the force between two objects that are moving relative to each other.
Static friction - Is the force of friction that keeps an object stationary so it does not move.
Different types of forces!
Newton's laws!
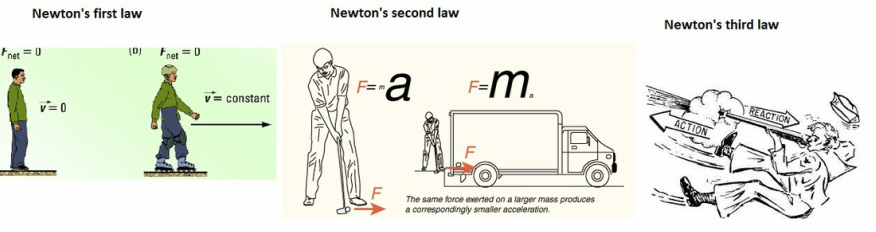
Newton's first law: An object will continue either being at rest or moving at a constant velocity unless acted upon by an external net force that isn't zero.
If Fnet = 0, then v = 0
Newton's second law: When an external non-zero net force acts on an object, the object accelerates in the direction of the net force. The magnitude of the acceleration is directly proportional to the magnitude of the net force and inversely proportional to the mass of the object.
Fnet = ma
Newton's third law: If object A exerts a force on object B, then B exerts a force on A that is equal in magnitude and opposite in direction.
Fa on b = -Fb on a
If Fnet = 0, then v = 0
Newton's second law: When an external non-zero net force acts on an object, the object accelerates in the direction of the net force. The magnitude of the acceleration is directly proportional to the magnitude of the net force and inversely proportional to the mass of the object.
Fnet = ma
Newton's third law: If object A exerts a force on object B, then B exerts a force on A that is equal in magnitude and opposite in direction.
Fa on b = -Fb on a
Friction Affects Motion
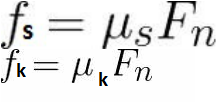
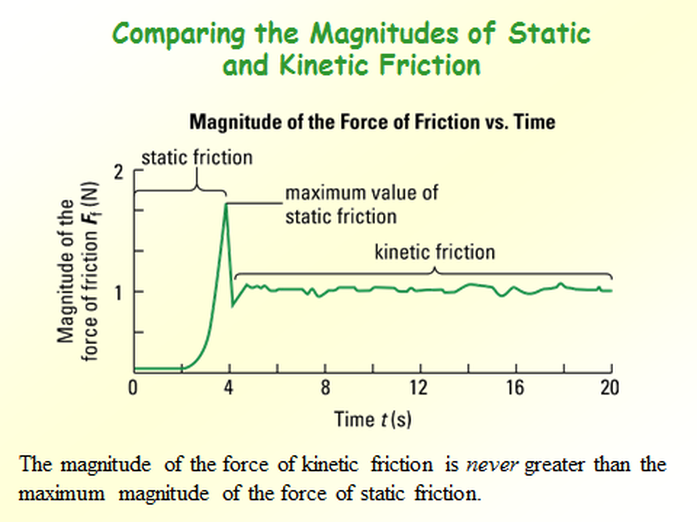
The main concepts in this sub chapter are kinetic friction, static friction, coefficient of static friction and coefficient of kinetic friction.
What is static friction? Its the force of friction that keeps an object stationary so it does not move.
What is kinetic friction? Kinetic friction is the force between two objects that are moving relative to each other.
Coefficient of static friction
Coefficient of kinetic friction
What is static friction? Its the force of friction that keeps an object stationary so it does not move.
What is kinetic friction? Kinetic friction is the force between two objects that are moving relative to each other.
Coefficient of static friction
Coefficient of kinetic friction
Gravity

Terminology
Gravitational mass - is the mass measured by comparing the weight of one object to an unknown object
Gravitationalforce - attraction between any two objects due to their mass
action-at-a-distance force - force that acts even if the objects involved are not touching
Field - three dimensional sphere
Gravitational field - surround any object that has a mass
Gravitational field strength - Is the name for the g-value (lowercase g) that we have for a particular region of space and is measure in m/s2, ex earth's is Earth's Gravitational field strength is 9.8 Newtons/kilogram.
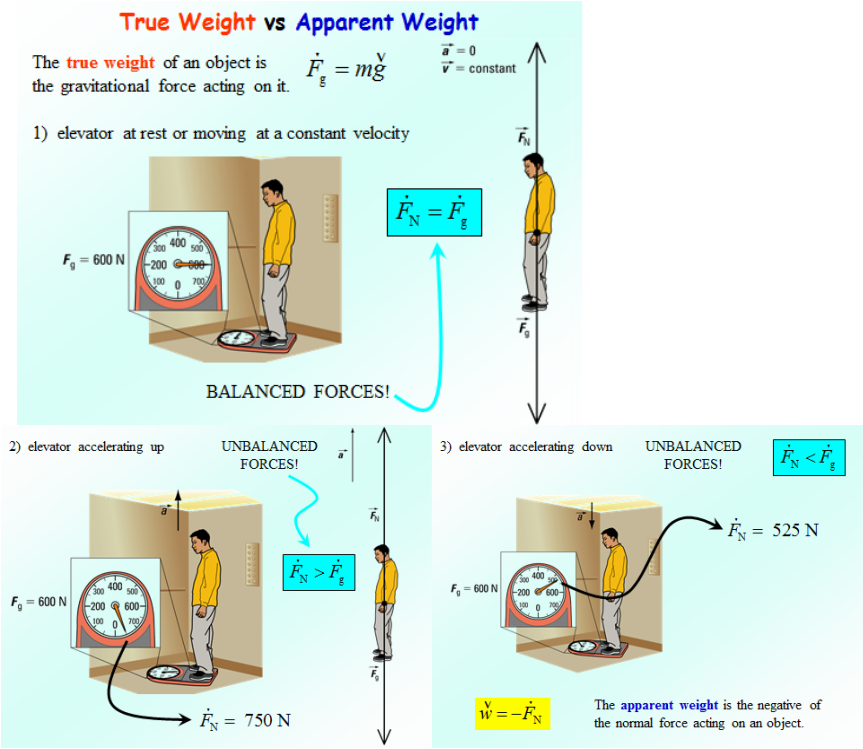
Apparent weight - The negative of the normal force acting on an object
True weight - Is the gravitational force acting on an object
Free fall - A free falling object is an object that is falling under the sole influence of gravity.
True weightlessness - A state in which an object has no actual weight (because it is in space and unaffected by gravitational attraction) or no apparent weight
Universal gravitational constant - G = 6.67 x 10 ^ -11 N x m^2/kg^2. This is a constant and will never change.
Newton's law of gravity

True weight and Apparent Weight
Unit 2: Questions
Key note - Mass is measured in kg, force is measured in N
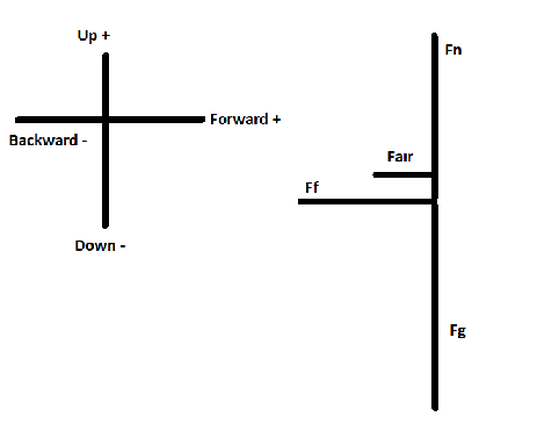
1. The driver in example 3.1 sees a pedestrian and steps on the brakes. The force of air resistance is 2500N backward. With the brakes engaged, the force of friction exerted on the car is 5000 N backward. Draw a free-body diagram for this situation.
2. The total weight of a biker and her motorbike is 1800 N down. With the engine engaged, the force of friction exerted by the road on the tires is 500N forward. The air resistance acting on the biker and the bike is 200N backward. The normal force exerted by the road on the biker and bike is 1800 N up. Calculate the net force.
Answer:
1800N up - 1800N down = 0 N, they cancelled each other out
500N forward - 200N backward = 300 N forward
Answer 300 N forward.
3. The net force acting on a 6.0 kg grocery cart is 12N [left]. Calculate the acceleration of the cart
Answer:
Fnet = ma
a = Fnet / m
a =12n / 6.0 kg
a = 2.0 m/s^2 left
4. A net force of 34 N forward acts on a curling stone causing it to accelerate at 1.8 m/s^2 forward on a frictionless icy surface. Calculate the mass of the curling stone.
Answer:
Fnet = ma
m = Fnet / a
m = 34N / 1.8 m/s ^ 2
m = 19 kg
5.An electric chain hoist in a garage exerts a force of 2.85 x 10^3 N up on an engine to remove it from a car. The acceleration of the engine is 1.50 m/s ^ 2 up. What is the mass of the engine.
Answer:
Fnet = Ft + Fg
ma = Ft + Fg
m = Ft / g + a
m = 2850 / (9.81 m/s^2 + 1.5 m/s^2)
m = 252 kg
6. Two boxes, A and B, are touching each other and are at rest on a horizontal frictionless surface, Box A has a mass of 25 kg and box B a mass of 15 kg. A person applies a force of 30N right on box A which, in turn, pushes on box B. Calculate the acceleration of the boxes.
Answer:
mt = ma + mb
mt = 40kg
Fnet = ma
a = Fnet / M
a = 30N / 40 kg
a = .75 m/s ^ 2
7.A 4.0 kg oak block on a horizontal, rough oak surface is attached by a light string that passes over a light, frictionless pulley to a hanging 2.0 kg object. The magnitude of the force of friction on the 4.0 kg block is 11.8 N. Calculate acceleration.
Answer:
a = [m1g-f]/(m1+m2)
a = 2.0 g x 9.81 m/s ^ 2 / 6.0 kg
a = 1.3 m/s ^ 2
T - f = m2a
8. Three men are pulling on ropes to a stationary crate. The first man exerts a force of 60.0 N north, the second a force of 35.0 N east, and the third a force of 45.0 N
at 30.0o east of south. What is the magnitude and direction of the net force acting on the crate?
Answer:
61.2 N at 20.1 degrees
9. A 50.0 kg crate rests on a floor. Jack exerts a force of 75.0 N north on the crate and Jill exerts a force of 100.0 N east on the crate. What is the magnitude and
direction of the acceleration which the crate undergoes while they pull?
Answer: 28.6 N
10. A man pushes on a 75.0 kg box such that his force of 225 N is exerted at an angle of 27.0 t the horizontal. If the floor exerts a frictional force of 44.0 N on the box, what is the net force acting on the box? If the box is initially at rest, how far will it have been pushed in 5.00 s
assuming those forces continued?
Answer: 156.5 N , 26.1 m
11. Two forces act on an object of mass 65.5 kg. One force is 500. N at an angle of 0.0. The object is accelerating at 2.00 m/s2 @ 90.0o. What is the magnitude and direction of a second force acting on the object?
Answer: 517 N at 165.3 degrees
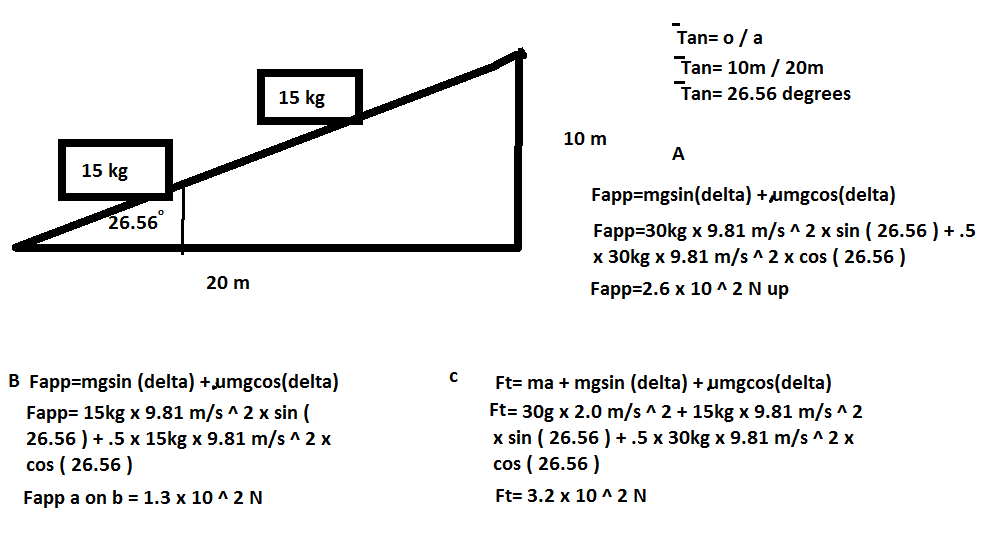
12. A roofer is shingling a roof that rises 1.0m vertical led every 2.0m horizontally. The roofer is pulling one bundle of shingles A with a rope up the roof. Another rope connects bundle A to bundle B farther down the roof. Each of the two bundles of shingles has a mass of 15kg. The coefficient of kinetic friction for the bundles on plywood sheeting is .50. What force must the roofer exert up the roof to drag the bundles at a constant speed. Calculate the force exerted by bundle A on B. What toal force would the roofer have to exert to accelerate both bundles to 2.0 m/s ^ 2 up.
Answer:
2. The total weight of a biker and her motorbike is 1800 N down. With the engine engaged, the force of friction exerted by the road on the tires is 500N forward. The air resistance acting on the biker and the bike is 200N backward. The normal force exerted by the road on the biker and bike is 1800 N up. Calculate the net force.
Answer:
1800N up - 1800N down = 0 N, they cancelled each other out
500N forward - 200N backward = 300 N forward
Answer 300 N forward.
3. The net force acting on a 6.0 kg grocery cart is 12N [left]. Calculate the acceleration of the cart
Answer:
Fnet = ma
a = Fnet / m
a =12n / 6.0 kg
a = 2.0 m/s^2 left
4. A net force of 34 N forward acts on a curling stone causing it to accelerate at 1.8 m/s^2 forward on a frictionless icy surface. Calculate the mass of the curling stone.
Answer:
Fnet = ma
m = Fnet / a
m = 34N / 1.8 m/s ^ 2
m = 19 kg
5.An electric chain hoist in a garage exerts a force of 2.85 x 10^3 N up on an engine to remove it from a car. The acceleration of the engine is 1.50 m/s ^ 2 up. What is the mass of the engine.
Answer:
Fnet = Ft + Fg
ma = Ft + Fg
m = Ft / g + a
m = 2850 / (9.81 m/s^2 + 1.5 m/s^2)
m = 252 kg
6. Two boxes, A and B, are touching each other and are at rest on a horizontal frictionless surface, Box A has a mass of 25 kg and box B a mass of 15 kg. A person applies a force of 30N right on box A which, in turn, pushes on box B. Calculate the acceleration of the boxes.
Answer:
mt = ma + mb
mt = 40kg
Fnet = ma
a = Fnet / M
a = 30N / 40 kg
a = .75 m/s ^ 2
7.A 4.0 kg oak block on a horizontal, rough oak surface is attached by a light string that passes over a light, frictionless pulley to a hanging 2.0 kg object. The magnitude of the force of friction on the 4.0 kg block is 11.8 N. Calculate acceleration.
Answer:
a = [m1g-f]/(m1+m2)
a = 2.0 g x 9.81 m/s ^ 2 / 6.0 kg
a = 1.3 m/s ^ 2
T - f = m2a
8. Three men are pulling on ropes to a stationary crate. The first man exerts a force of 60.0 N north, the second a force of 35.0 N east, and the third a force of 45.0 N
at 30.0o east of south. What is the magnitude and direction of the net force acting on the crate?
Answer:
61.2 N at 20.1 degrees
9. A 50.0 kg crate rests on a floor. Jack exerts a force of 75.0 N north on the crate and Jill exerts a force of 100.0 N east on the crate. What is the magnitude and
direction of the acceleration which the crate undergoes while they pull?
Answer: 28.6 N
10. A man pushes on a 75.0 kg box such that his force of 225 N is exerted at an angle of 27.0 t the horizontal. If the floor exerts a frictional force of 44.0 N on the box, what is the net force acting on the box? If the box is initially at rest, how far will it have been pushed in 5.00 s
assuming those forces continued?
Answer: 156.5 N , 26.1 m
11. Two forces act on an object of mass 65.5 kg. One force is 500. N at an angle of 0.0. The object is accelerating at 2.00 m/s2 @ 90.0o. What is the magnitude and direction of a second force acting on the object?
Answer: 517 N at 165.3 degrees
12. A roofer is shingling a roof that rises 1.0m vertical led every 2.0m horizontally. The roofer is pulling one bundle of shingles A with a rope up the roof. Another rope connects bundle A to bundle B farther down the roof. Each of the two bundles of shingles has a mass of 15kg. The coefficient of kinetic friction for the bundles on plywood sheeting is .50. What force must the roofer exert up the roof to drag the bundles at a constant speed. Calculate the force exerted by bundle A on B. What toal force would the roofer have to exert to accelerate both bundles to 2.0 m/s ^ 2 up.
Answer:
13 . Two people, A and B, are sitting on a bench .60m apart. Person A has a mass of 55 kg and person B has a mass of 80 kg. Calculate the magnitude of the gravitational field strength.
Answer:
Fg = Gm1m2 / r^2
Fg = 6.67 x 10 ^ -11N x 55kg x 80kg / .60m ^ 2
Fg = 8.2 x 10 ^ -7 N
14. The mass of the Titanic was 4.6 x 10 ^ 7 kg, suppose the magnitude of the gravitational force exerted by the Titanic on the fatal iceberg was 61 N when the separation distance was 100m. What was the mass of the iceberg?
Answer:
g = Gm1m2 / r ^ 2
m1 = g x r ^ 2 / G x m2
m1 = 2.0 x 10 ^ 8 kg
15. Object A exerts a gravitational force of magnitude 5.9 x 10 ^ -11 N on object B. For each situation, determine the magnitude of the gravitational force. Explain your reasoning. The separation distance increase to 4/3 of its original value, ma increases to 3/2 of its original value and mb is halved. The separation distance decreases to 1/6 of its original value, ma is halved, and mb increased to 5/4 of its original value.
Answer: Part 1
Fg = Gm1m2 / r ^ 2
Fg = 5.9 x 10 ^ -11N x 1.5 kg x .5 kg / 1.3 ^ 2
Fg = 2.5 x 10 ^ -11 N
Part 2
Fg = Gm1m2 / r ^2
Fg = 5.9 x 10 ^ -11 N x .5 kg x 1.25 kg / .167m ^ 2
Fg = 1.3 x 10 ^ -9 N
16. A Satellite is orbits Earth at a distance of 3r above Earths surface. How many Earth radii is the satellite from Earth's center?
Answer:
4r
17. An 80 kg astronaut is in orbit 4.20 x 10 ^ 4 km from Earth's center. Calculate the magnitude of gravitational field strength at the location of the astronaut. What would be the magnitude of the gravitational field strength if the astronaut is orbiting the moon with the same separation distance.
Answer:
g =Gm1 / r ^ 2
g = 6.67 x 10 ^ -11 N x 5.97 x 10 ^ 24 kg / 32000000 m ^ 2
g = 3.89 x 10 ^ -1 N/kg
Answer:
g =Gm1 / r ^ 2
g = 6.67 x 10 ^ -11 N x 7.35 x 10 ^ 22 kg
g = 4.79 x 10 ^ -4 N/kg
18. A 60.0 kg astronaut is standing on a scale in a rocket about to land on the surface of Mars. The rocket slows down at 11.1 m/s 2 while approaching Mars. Calculate the true weight and apparent weight of the astronaut as the rocket lands, and if the rocket is accelerating at 7.38 m/s ^ 2 up when leaving mars.
Answer: Part 1
True weight
Fg = mg
Fg = 60.0 kg x 3.7 m/s ^ 2
Fg = 2.22 x 10 ^ 2 N
Apparent weight
g =Gm1 / r ^ 2
g = 6.67 x 10 ^ -11 N x 6.42 x 10 ^ 23 / 3.40 x 10 ^ 6 squared
g = 3.7 m/s ^ 2
Fnet = Fn + Fg
Fn = ma = Fg
Fn = 60.0 kg x 11.1m/s + 60.0 kg x 3.7 m/s ^ 2
Fn = 8.88 x 10 ^ 2 N
Answer: Part 2
True
Fg = 60.0 kg x 3.7 m/s ^ 2
Fg = 2.22 x 10 ^ 2 N
Apparent weight
Fnet = Fn + Fg
Fn = ma + Fg
Fn = 60.0 kg x 7.38 m/s ^ 2 + 60.0 kg x 3.7 m/s ^ 2
Fn = 6.65 x 10 ^ 2 N
Answer:
Fg = Gm1m2 / r^2
Fg = 6.67 x 10 ^ -11N x 55kg x 80kg / .60m ^ 2
Fg = 8.2 x 10 ^ -7 N
14. The mass of the Titanic was 4.6 x 10 ^ 7 kg, suppose the magnitude of the gravitational force exerted by the Titanic on the fatal iceberg was 61 N when the separation distance was 100m. What was the mass of the iceberg?
Answer:
g = Gm1m2 / r ^ 2
m1 = g x r ^ 2 / G x m2
m1 = 2.0 x 10 ^ 8 kg
15. Object A exerts a gravitational force of magnitude 5.9 x 10 ^ -11 N on object B. For each situation, determine the magnitude of the gravitational force. Explain your reasoning. The separation distance increase to 4/3 of its original value, ma increases to 3/2 of its original value and mb is halved. The separation distance decreases to 1/6 of its original value, ma is halved, and mb increased to 5/4 of its original value.
Answer: Part 1
Fg = Gm1m2 / r ^ 2
Fg = 5.9 x 10 ^ -11N x 1.5 kg x .5 kg / 1.3 ^ 2
Fg = 2.5 x 10 ^ -11 N
Part 2
Fg = Gm1m2 / r ^2
Fg = 5.9 x 10 ^ -11 N x .5 kg x 1.25 kg / .167m ^ 2
Fg = 1.3 x 10 ^ -9 N
16. A Satellite is orbits Earth at a distance of 3r above Earths surface. How many Earth radii is the satellite from Earth's center?
Answer:
4r
17. An 80 kg astronaut is in orbit 4.20 x 10 ^ 4 km from Earth's center. Calculate the magnitude of gravitational field strength at the location of the astronaut. What would be the magnitude of the gravitational field strength if the astronaut is orbiting the moon with the same separation distance.
Answer:
g =Gm1 / r ^ 2
g = 6.67 x 10 ^ -11 N x 5.97 x 10 ^ 24 kg / 32000000 m ^ 2
g = 3.89 x 10 ^ -1 N/kg
Answer:
g =Gm1 / r ^ 2
g = 6.67 x 10 ^ -11 N x 7.35 x 10 ^ 22 kg
g = 4.79 x 10 ^ -4 N/kg
18. A 60.0 kg astronaut is standing on a scale in a rocket about to land on the surface of Mars. The rocket slows down at 11.1 m/s 2 while approaching Mars. Calculate the true weight and apparent weight of the astronaut as the rocket lands, and if the rocket is accelerating at 7.38 m/s ^ 2 up when leaving mars.
Answer: Part 1
True weight
Fg = mg
Fg = 60.0 kg x 3.7 m/s ^ 2
Fg = 2.22 x 10 ^ 2 N
Apparent weight
g =Gm1 / r ^ 2
g = 6.67 x 10 ^ -11 N x 6.42 x 10 ^ 23 / 3.40 x 10 ^ 6 squared
g = 3.7 m/s ^ 2
Fnet = Fn + Fg
Fn = ma = Fg
Fn = 60.0 kg x 11.1m/s + 60.0 kg x 3.7 m/s ^ 2
Fn = 8.88 x 10 ^ 2 N
Answer: Part 2
True
Fg = 60.0 kg x 3.7 m/s ^ 2
Fg = 2.22 x 10 ^ 2 N
Apparent weight
Fnet = Fn + Fg
Fn = ma + Fg
Fn = 60.0 kg x 7.38 m/s ^ 2 + 60.0 kg x 3.7 m/s ^ 2
Fn = 6.65 x 10 ^ 2 N